纹理图像是我们日常生活中十分常见的一种图像类型，如壁纸、地砖、布艺等。纹理图像分析在纺织工艺、印刷、指纹识别、材料设计和生物形态学分析等领域有重要应用。除了图像的灰度值、光滑性等基本信息外，我们有时更关注纹理图像的细节、边界、重复结构等数字化特征。

图 1 纹理图像示例

纹理图像有三个基本特征：局部周期性、非随机性平面嵌入、有限区域内均匀统一。图像的纹理信息是除了色度外最重要的数字特征。同样的色度但不同周期性结构的纹理图像会给人带来不一样视觉效果。例如，在纺织工艺中，通过设计不同的图案基元，可以生产平纹、斜纹、镂空、提花等纹理织物[2]。一般情况下，纹理织物的数字化特征取决于图案基元的周期性分布方式。如图 1 所示，纹理织物是由相同或相似的图案基元按照一定的规则在二维平面上周期性地排列而成。

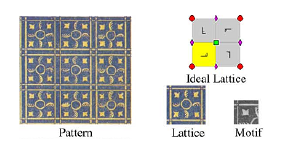
图 2 纹理图像的构成

图像的特征提取已广泛应用于计算机视觉处理的各个分支，而识别纹理图像的基本单元是图像分析的一项重要研究内容。纹理织物可以视为晶格（Lattice）在二维平面中的嵌入，而晶格又可进一步分解为更小的图案基元（Motif）。图案基元有三角形、矩形和平行四边形三种形式。一个给定的图案基元在二维平面中通过平移、镜像、旋转、滑动镜像四种变换可以构成一个晶格。图 2 展示了一幅纹理织物图像及其对应的图案基元和晶格。根据图案基元和晶格之间的位置关系，几何学家借助群论概念证明了纹理织物共有 17 类，亦称为平面对称群或壁纸群[5]。图 3 展示了 17 类壁纸群的图案基元和晶格的几何缩略图[8]，其中符号 p，c 分别表示初始单元格和以面为中心的单元格，接下来的数字表示旋转变换的次数；符号 m 和 g 分别表示镜像和滑动镜像变换。纹理织物中图案基元的细微差别可能导致它们分属于不同的类别，而灰度值、晶格大小、排列规则迥异的两种纹理织物可能属于同一类。如图 1 中的 (c) 和 (d) 两幅视觉效果不同的纹理织物却同属于 p4 类。

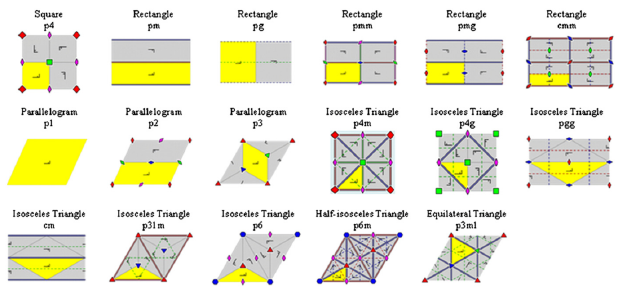
图 3 17类平面对称群

1 瑕疵检测问题

在纺织生产中，纹理织物在织造过程中可能会出现扭结、划痕、破洞、污损等瑕疵（如图 4）。如何精准地、高效地检测出纹理织物中的瑕疵大小、位置以及种类，对于提高产品质量、资源利用率和生产效率有着重要的经济意义。人工方式的瑕疵检测具有劳动强度大、检测效率低、瑕疵的甄别或分类易受主观因素影响等缺点，很难满足工业生产的要求。随着计算机视觉和模式识别技术的发展，建立纺织品的自动化视觉检测（Automated Visual Inspection, AVI）系统是纺织科学与织造工艺中的一项重要研究内容。因此，纹理图像的图像分析、模式识别和特征提取等在自动化视觉的瑕疵检测中发挥着重要作用。

图 4 有瑕疵的纹理织物

给定一幅图像，纹理分析的目的是将图像分解成统计性质无关的 cartoon 部分和 texture 部分的叠加。图 5 中的 cartoon 呈现了图像的轮廓、平滑结构及灰度值等信息；texture 则包含了图像的纹理、细节及重复结构等信息。尽管 cartoon 与 texture 的函数性质迥异（前者具有分片光滑性，后者具有高频周期性），二者在 Sobolev 空间范数下都具有稀疏结构\cite{Aujol06}。具体地，给定一幅图像的向量化表示 ， 空间中的半范数 （即全变差范数）可以用于正则化图像的分片光滑部分，而其对偶范数（左右滑动查看公式）

可以用于正则化图像的高频振荡部分。

图 5 纹理织物的 cartoon 和 texture 部分

AVI 系统借助图像分析技术来检测纹理织物中的瑕疵有两类方法：图案基元类和非图案基元类方法（见综述 [4]）:

• 图案基元类的方法: 在已知图案基元的前提下，借助晶格的周期性结构和图像处理中的滤波器等工具，鉴别纹理中潜在的瑕疵区域。由于 p1 类纹理的图像函数具有各项同性的特点，针对 p1 类纹理的瑕疵检测已有较为成熟的算法，包括基于自相关函数、共生（Co-occurrence）矩阵、马尔科夫随机场的统计类方法；基于数学分形和形态学分析的计算几何类方法；基于自回归、神经网络的机器学习类方法；基于统计分类的 Bollinger band（BB） 方法和 Regular band（RB） 方法等。

• 非图案基元类方法: 当图案基元未知或较难提取时，分析纹理图像在某种变换下的稀疏性（如 Fourier, wavelets, Gabor 变换等）、周期性、低秩性等特点，建立极小能量函数，获取优化模型的最优解。由于非 p1 类纹理的图像函数具有各项异性（anisotropy）的特点，其相应的瑕疵检测问题较为困难。目前，有一系列针对特定类别纹理的瑕疵检测方法，如针对镂空类织物的图像反馈法、提花类织物的 Hash 函数法、p2、p4m 和 pmm 类织物的 Gabor 变换法等。

数学优化模型

晶格在纹理织物中的周期性排列，反映出纹理织物具有 texture 的性质。基于纹理分析技术，建立瑕疵检测的数学模型，设计快速稳健的优化算法来精确地、高效地识别织物中的瑕疵，对纺织生产有重要意义。

• 对于高频的纹理织物，由于其图像函数具有各项异性的特点，图像函数可以表示为 ，其中  是带有瑕疵的纹理图像， 表示瑕疵（在时域下有稀疏性）， 是纹理图像（具有低秩性或谐波变换下的稀疏性），如图 6 所示。利用经典图像分解模型可以处理该情形下的瑕疵检测问题。例如，基于 Sobolev 空间半范数的模型[1]

基于谐波函数的 TV-curvelets 模型[3]

基于低秩矩阵的优化模型[6]

基于各项异性非线性扩散张量的模型 [7] 等。

• 对于低频的纹理织物，图像分解方法理论上很难把 cartoon 和低频 texture 分开。假设纹理织物的晶格已知（如用统计类或机器学习类方法提取），可以利用晶格、Dirac函数构成的0-1矩阵的卷积刻画纹理织物，用分片常数函数刻画瑕疵，具体的数学关系式为 ，其中， 是图案晶格， 表示卷积运算， 是 Dirac 函数在离散形式下对应的0-1矩阵 （如图 7 所示）。

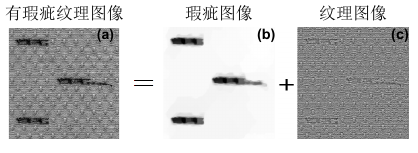
图 6 图像分解法实现纹理织物的瑕疵检测

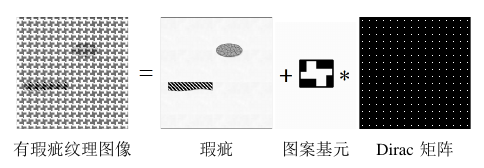
图 7 Dirac 函数法实现纹理织物的瑕疵检测[14]

无论采用何种形式的正则化函数，纹理织物瑕疵检测中的数学模型大多可以归结为如下形式的优化问题

其中，,  和   均是正常下半连续函数（可能非凸或非光滑）， 和  为简单约束集合。 通常是瑕疵图像的正则化函数（如全变差、组稀疏、小波变换等）， 为纹理图像的正则化函数（如 Sobolev 空间中半范数、曲波变换、矩阵低秩函数等）， 刻画上述函数关系式中的拟合程度。

AVI 系统进行瑕疵检测的目标是建立实时的检测机制，这就对优化方法的时效性有很高的要求。因此，设计高效的、量身定制的数值优化算法求解优化问题 ，对解决纹理织物特征提取和瑕疵检测有重要意义。

参考文献

[1] J.F. Aujol, G. Gilboa, T. Chan, S. Osher, Structure-texture image decomposition–modeling, algorithms, and parameter selection, Int. J. Comput. Vision, 67 (2006), 111-136. 

[2] A. R. Horrocks, S. C. Anand, Handbook of Technical Textiles, Elsevier, 2000. 

[3] P. Maure, J.F. Aujol, and G. Peyre,´ Locally parallel texture modeling, SIAM J. Imaging Sci., 4 (2011), 413-447. 

[4] H.Y. Ngan, G.K. Pang, N.H. Yung, Automated fabric defect detection–a review, Image Vision Comput., 29 (2011), 442-458. 

[5] R.L.E. Schwarzenberger, The 17 plane symmetry groups, Math. Gaz. 58, 1974.

[6] H. Schaeffer, S. Osher, A low patch-rank interpretation of texture, SIAM J. Imaging Sci., 6 (2013), 226-262. 

[7] J. Weickert, Anisotropic Diffusion in Image Processing, Teubner Stuttgart, 1998. 

[8] Wikipedia, http://en.wikipedia.org/wiki/Wallpaper group, 2010. 

[9] M.K. Ng, X.M. Yuan, W.X. Zhang, Coupled variational image decomposition and restoration model for blurred cartoon-plus-texture images with missing pixels, IEEE Trans. Image Process., 22 (2013), 2233-2246. 

[10] M.K. Ng, H.Y. Ngan, X.M. Yuan, W.X. Zhang, Patterned fabric inspection and visualization by texture and defect decomposition method, IEEE Trans. Autom. Sci. Eng.,11 (2014), 943-947. 

[11] D.R. Han, X.M. Yuan, W.X. Zhang, An augmented Lagrangian based parallel splitting method for separable convex minimization with applications to image processing, Math. Comput., 83 (2014), 2263-2291 

[12] D.R. Han, W.W. Kong, W.X. Zhang, A partial splitting augmented Lagrangian method for low-patch-rank image decomposition, J. Math. Imaging Vision, 51 (2015), 145-160. 

[13] Y.H. Dai, D.R. Han, X.M. Yuan, W.X. Zhang, A sequential updating scheme of Lagrange multiplier for separable convex programming, Math. Comput., 86 (2017), 315-343. 

[14] M.K. Ng, H.Y.T. Ngan, X.M. Yuan, W.X. Zhang, Lattice-based patterned fabric inspection by using total variation and sparsity with low-rank representations, SIAM J. Imaging Sci., 10 (2017), 2140-2164

排版：柚子美编一号（西交大金融优化组夏川）

如需转载请联系公众号