来自华为诺亚方舟实验室、北京大学、悉尼大学的研究者提出了一种受量子力学启发的视觉 MLP 新架构。

近年来，计算机视觉领域的新型架构层出不穷，包括视觉 Transformer、MLP 等，它们在很多任务上都取得了超越 CNN 的性能，受到广泛关注。其中，视觉 MLP 具有极其简单的架构，它仅由多层感知器（MLP）堆叠而成。与 CNN 和 Transformer 相比，这些简洁的 MLP 架构引入了更少的归纳偏置，具有更强的泛化性能。

然而，现有视觉 MLP 架构的性能依然弱于 CNN 和 Transformer。来自华为诺亚方舟实验室、北京大学、悉尼大学的研究者提出了一种受量子力学启发的视觉 MLP 架构，在 ImageNet 分类、COCO 检测、ADE20K 分割等多个任务上取得了 SOTA 性能。

论文地址：https://arxiv.org/abs/2111.12294

PyTorch 代码：https://github.com/huawei-noah/CV-Backbones/tree/master/wavemlp_pytorch

MindSpore 代码：https://gitee.com/mindspore/models/tree/master/research/cv/wave_mlp

Wave-MLP

该研究受量子力学中波粒二象性的启发，将 MLP 中每个图像块 (Token) 表示成波函数的形式，从而提出了一个新型的视觉 MLP 架构——Wave-MLP，在性能上大幅超越了现有 MLP 架构以及 Transformer。

量子力学是描述微观粒子运动规律的物理学分支，经典力学可被视为量子力学的特例。量子力学的一个基本属性是波粒二象性，即所有的个体（比如电子、光子、原子等）都可以同时使用粒子的术语和波的术语来描述。一个波通常包括幅值和相位两个属性，幅值表示一个波可能达到的最大强度，相位指示着当前处在一个周期的哪个位置。将一个经典意义上的粒子用波（比如，德布罗意波）的形式来表示，可以更完备地描述微观粒子的运动状态。

那么，对于视觉 MLP 中的图像块，能不能也把它表示成波的形式呢？该研究用幅值表达每个 Token 所包含的实际信息，用相位来表示这个 Token 当前所处的状态。在聚集不同 Token 信息的时候，不同 Token 之间的相位差会调制它们之间的聚合过程（如图 3 示）。考虑到来自不同输入图像的 Token 包含不同的语义内容，该研究使用一个简单的全连接模块来动态估计每个 Token 的相位。对于同时带有幅度和相位信息的 Token，作者提出了一个相位感知 Token 混合模块（PATM，如下图 1 所示）来聚合它们的信息。交替堆叠 PATM 模块和 MLP 模块构成了整个 Wave-MLP 架构。

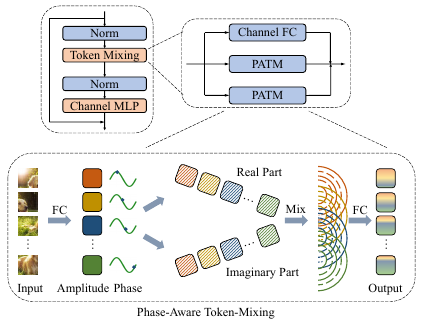
图 1：Wave-MLP 架构中的一个单元

相比现有的视觉 Transformer 和 MLP 架构，Wave-MLP 有着明显的性能优势（如下图 2 所示）。在 ImageNet，Wave-MLP-S 模型上以 4.5G FLOPs 实现了 82.6% 的 top-1 准确率，比相似计算代价的 Swin-T 高 1.3 个点。此外，Wave-MLP 也可以推广到目标检测和语义分割等下游任务，展现出强大的泛化性能。

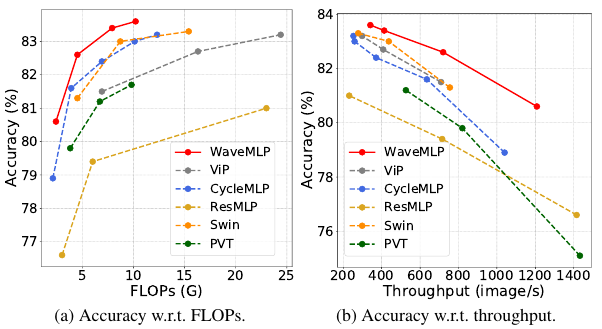
图 2：Wave-MLP 与现有视觉 Transformer、MLP 架构的比较

用波表示 Token

在 Wave-MLP 中，Token 被表示为同时具有幅值和相位信息的波，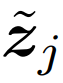

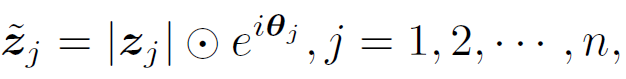    （1）

其中 i 是满足 i^2 = -1 的虚数单位，|·| 表示绝对值运算，⊙是逐元素乘法。幅值 |z_j| 是实值的特征，表示每个 Token 所包含的内容。θ_j 表示相位，即 Token 在一个波周期内的当前位置。

两个 Token 之间的相位差对它们的聚合过程有很大影响 （如下图 3 所示）。当两个 token 具有相同的相位时，它们会相互增强，得到幅值更大的波（图 3（b））；当两个 token 相位相反时，他们合成的波将相互减弱。在其他情况下，它们之间的相互作用更加复杂，但仍取决于相位差（图 3（a））。经典方法中使用实值表示 token 的，这实际上是上式的一个特例。

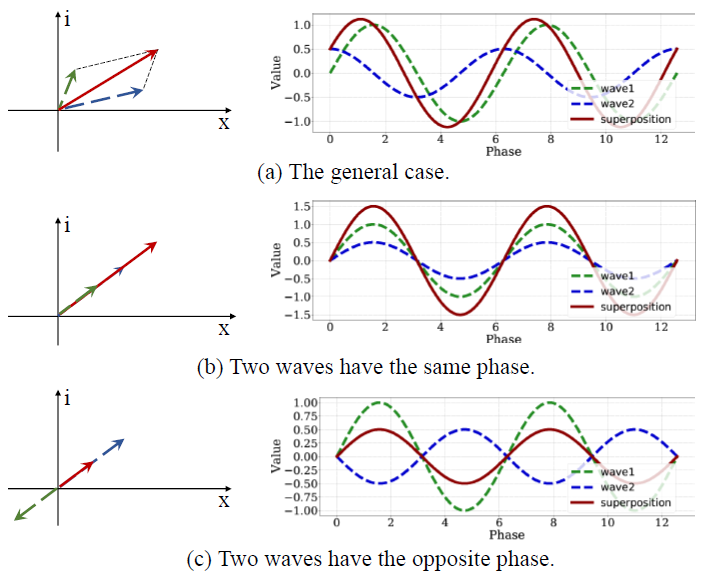
图 3：两个具有不同相位的波的聚合过程。左侧表示两个波在复数域中的叠加，右侧表示它们在实轴上的投影随着相位的变化。虚线表示两个初始相位不同的波，实线是他们的叠加。

相位感知的 Token 聚合

公式（1）中包含幅值和相位两项，幅值 z_j 类似于实值特征，可以采用标准的 Channel-FC 生成：

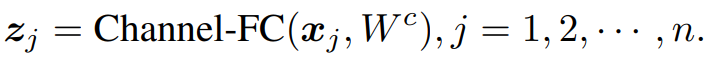    （2）

对于相位，可以使用多种方式来估计。为了使得相位可以捕获每个输入的特定属性，该研究使用一个可学的估计模块来生成相位 θ_j。在获得幅值 z_j 和相位 θ_j 之后，可以根据公式（1）得到 Token 的波函数表示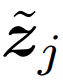。同时，公式（1）可以采用欧拉公式展开成连个实值向量拼接的形式：

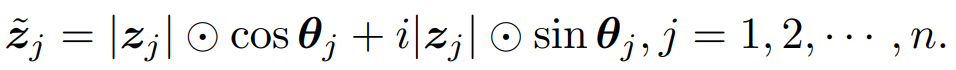    （3）

表示不同的 Token 波函数会通过一个 Token-FC 聚合起来，得到复数域的输出：

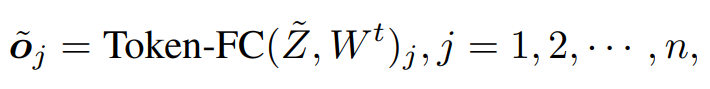    （4）

类似于量子计算中的测量过程，复数域的需要映射到实数域里才能得到有意义的输出值。将实部和虚部做按照一定的权重进行求和，得到模块的输出：

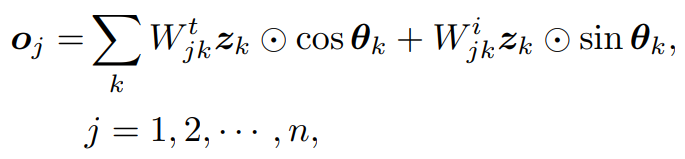    （5）

在视觉 MLP 中，该研究构建了一个相位感知模块（PATM，图 1）来完成 Token 聚合的过程。交替堆叠 PATM 模块和 channel-mixing MLP 组建了整个 WaveMLP 架构。

实验结果

该研究在大规模的分类数据集 ImageNet, 目标检测数据集 COCO 和语义分割数据集 ADE20K 上都进行了大量实验。

ImageNet 上图像分类的结果如表 1，表 2 所示：相比于现有的 Vision MLP 架构和 Transformer 架构，WaveMLP 都取得了明显的性能优势。

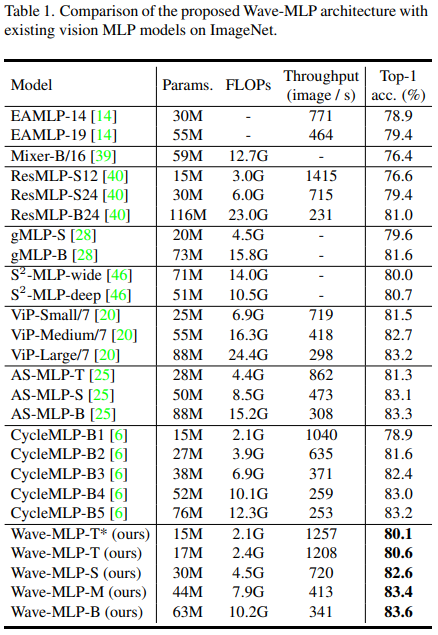
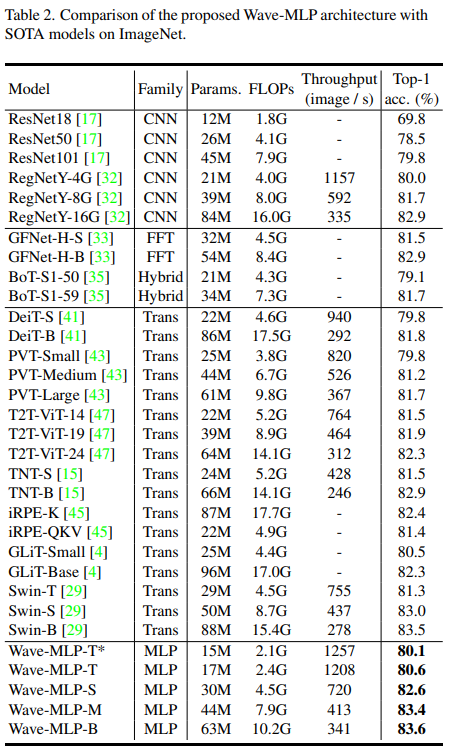
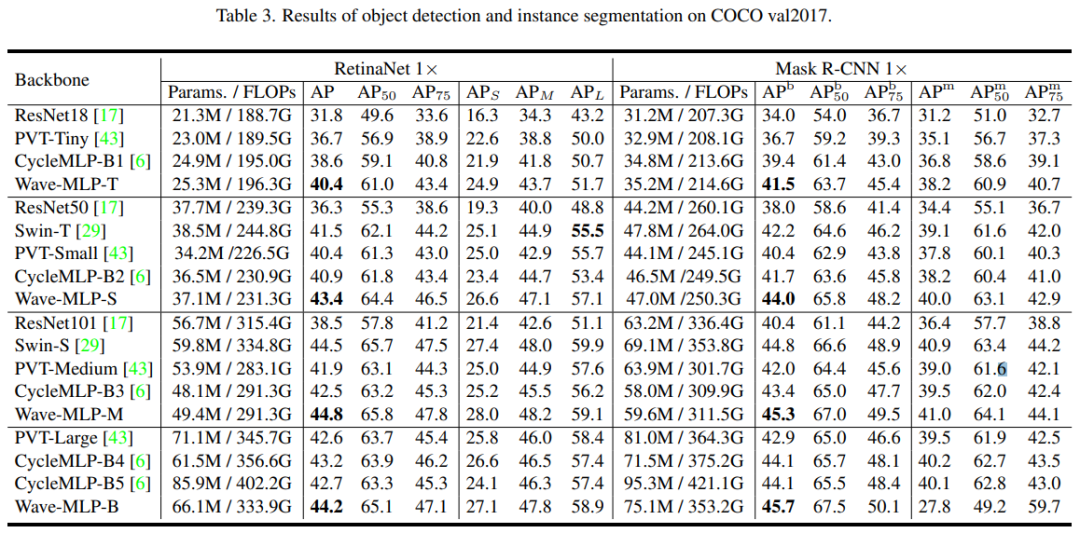
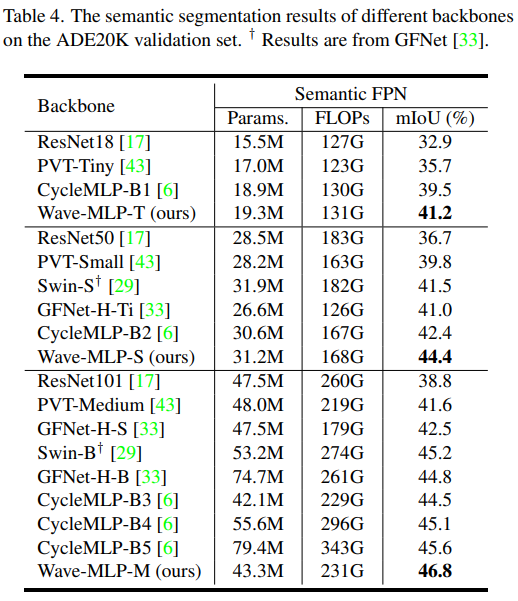
在下游目标检测、语义分割等任务中，Wave-MLP 同样表现出更优的性能。