论文链接：https://arxiv.org/pdf/1911.07524.pdf

开源地址：https://github.com/HuangJunJie2017/UDP-Pose

今天更新一篇经典论文的笔记，UDP方法是COCO 2020 Keypoint Detection Challenge的冠军方案中重要的组成部分，在比较早的时候我读过一次，写这篇笔记的契机是从知乎发现作者重写了这篇论文，对很多细节进行了完善，因此很适合写一篇完整的学习笔记。针对作者提出的问题，我自己设计了一些例子来帮助大家更好理解。

在阅读之前我假设读者至少具备以下知识：

• Heatmap-based方法的编码（渲染高斯热图）、解码（Argmax）过程及原理（监督方式）

• 姿态估计任务图像增强所进行的操作（各种图像变换）

前言

相较于其他的计算机视觉下游任务（如图像分类、目标检测、语义分割等），姿态估计评测算法性能的指标是直接基于坐标来计算的，因此，姿态估计任务对数据处理方法非常敏感，在选择数据处理方法时也需要谨慎，考虑到图像变换对应的标注信息转变。

然而在本文之前，并没有人指出当前大家常用的数据处理方法是存在问题的，大家的算法在数据处理这一步就无意识地引入了误差，从而导致结果不是最优的。尽管也有一部分人意识到了这种误差的存在，但解决的方案却停留在一种经验性地“土方法”的形式上，而这些“土方法”虽然能实实在在地涨点，却因为给不出合理的解释，很多项目都是悄悄地用而不书面说明，因而给算法精度的复现制造了很多麻烦。

最终，本文归纳性地提出了无偏数据处理方法（Unbiased Data Processing），总结了姿态估计任务中误差存在的两个方面：

• 数据增强引入的偏差

• 量化误差

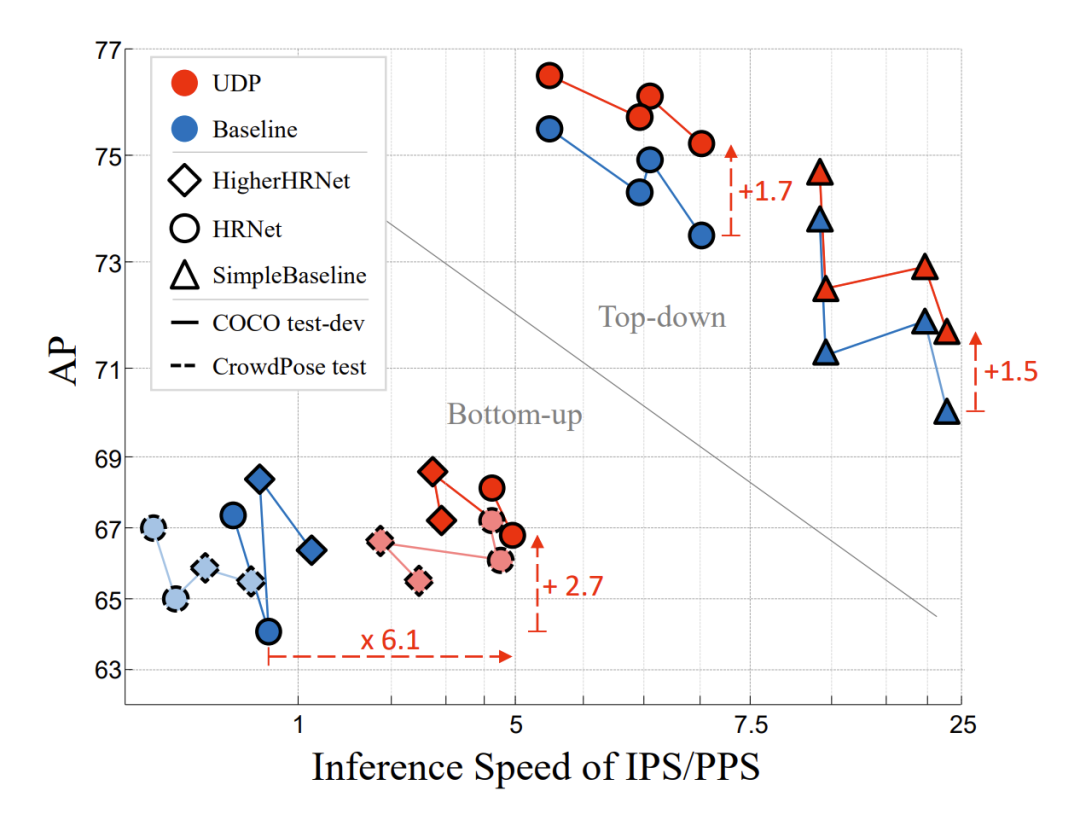
仅通过修正这些误差，在不提出任何新算法的情况下就让HRNet有了很大的性能提升，在top-down方案上涨了1.7AP，在bottom-up方案上涨了2.7AP。

我个人很喜欢作者为本文起的标题，因为非常地贴切，这种数据处理引入的误差很难被注意，即使明确指出来，要清楚理解也需要花一点功夫去思考，实在无愧于“藏在细节里的魔鬼”之称。

论文作者的感叹原话：

这个东西理解起来有点费劲，我自己也是一边写论文一边推明白（写论文之前也只有各大概的概念），所以真不能强求自己在几天内能看懂。如果能通过推理自己把论文里唯一的图画出来，你知道的就已经不比我少了。

“魔鬼”长什么样子

在过去的数据处理中，我们所使用的图片坐标系往往是基于像素的，由于图像是由一个个像素组成的矩阵，我们很自然地会使用像素所在的数组下标作为坐标，将图像的左上角作为坐标系的原点，用矩阵的长宽来代表图片的长宽。

当进行水平翻转(Flipping)操作时，我们的常规操作是：

joints_3d_flipped[:, 0] = img_width - 1 - joints_3d_flipped[:, 0]

即，翻转后坐标 = 图片宽度 - 1 - 原始坐标

在人体姿态估计任务中，非常普遍使用的一个技巧叫做翻转集成(flipping ensemble) ：对一张输入图片，会正向输入模型推理一次，再水平翻转图片后推理一次，翻转图片推理的结果再次翻转回去，将两次的结果取平均。这样能让模型的预测结果更加鲁棒，提升一定的准确度。

以上是背景知识，下面我用一个简单的例子来说明这种坐标系建立方式所存在的问题：

假如我们的原始图片尺寸为16x16，输入模型的图片尺寸为8x8，Heatmap-based方法通常输出的特征图会是4倍下采样，即输出特征图尺寸为2x2。

在原始图片上，我们有一个标注点(8, 8)，现在我想问，假如我们的模型预测是100%准确的，我把图片水平翻转后送入模型，将模型输出的结果水平翻转回来，理论上来说模型预测的坐标是多少？

不难计算，由于假设了模型不存在预测错误的情况，理论上两次水平翻转标注点位置不变，预测坐标应该是原始坐标经过8倍下采样，即(1, 1)。

可是按照传统的数据处理流程，结果会是：

• (8, 8)经过Resize到输入图片尺寸，为(4, 4)

• 进行一次水平翻转操作，坐标计算8 - 1 - 4 = 3得到(3, 4)

• 再经过4倍下采样，目标点对应的2x2特征图上的坐标为(0.75, 1)，由于模型输出的结果只能是整数，那么在这个只有0和1两个坐标值的坐标系里，因为0.75 > 0.5，坐标1对应的特征图像素上响应值会更大，因而模型输出解码为(1, 1)

• 再次水平翻转，2 - 1 - 1 = 0回到原始坐标，模型翻转预测的结果为(0, 1)

发现没有，经过我们的数据处理，最终模型预测的坐标跟标注对不上了，而且足足偏移了1个像素。

于是最终模型集成的结果理论上变成了(0.5, 1)，同样偏离了标注位置。

简单来说，由于下采样的关系，用像素个数来表示坐标轴刻度的方式，会在水平翻转时出现结果无法对齐的问题。

要知道在这个例子中，我还做出了模型100%准确这种非常强的假设，在实际情况中模型自身还有预测误差，该问题会被隐藏得更深。也因此我对作者敏锐的洞察力，以及溯源问题到坐标系定义上，佩服的五体投地。

在连续空间中定义图片

为了避免以上问题的出现，作者对整个图片坐标系进行了重新定义，提出在连续空间上定义图片，每一个像素只是连续空间上的一个采样点，因而图片的长宽不再是像素点的个数，而是根据单位长度来计算。

这样的变化有点类似于一片网格点，数方格和数线段交点的区别，在连续空间上，每一个线段交点就是一个像素采样点。按照这样的定义，图片的长宽会等于像素个数减1。

当图片发生变换时，由于坐标系上采样点的位置固定，因此就算采样点跟原来没有正好对应的像素，也可以通过插值得到变换后的像素值：

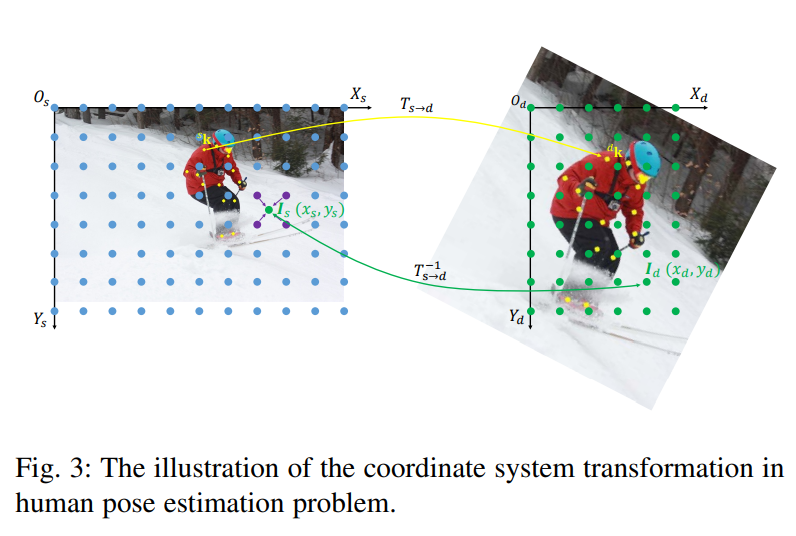
然后很自然地，我们可以推出四种常见图像变换矩阵：

Cropping

把图片坐标系的原点移动到ROI框的左上角：

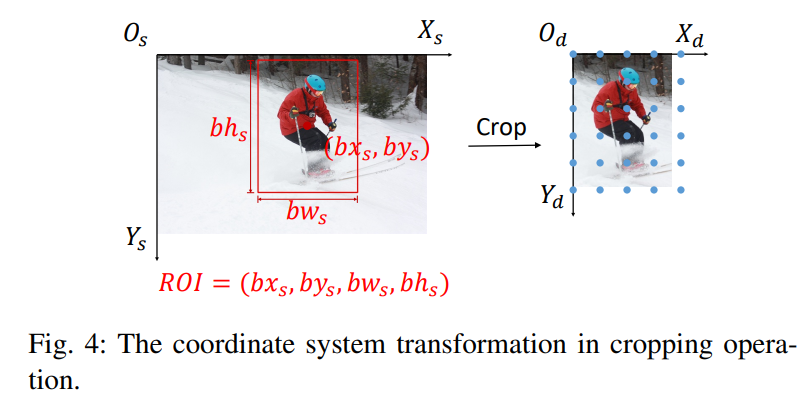
变换矩阵为：

Resizing

由于图片定义在连续空间上，因此只需要调整采样点的间距，即坐标系的单位长度，就能对图片进行缩放：

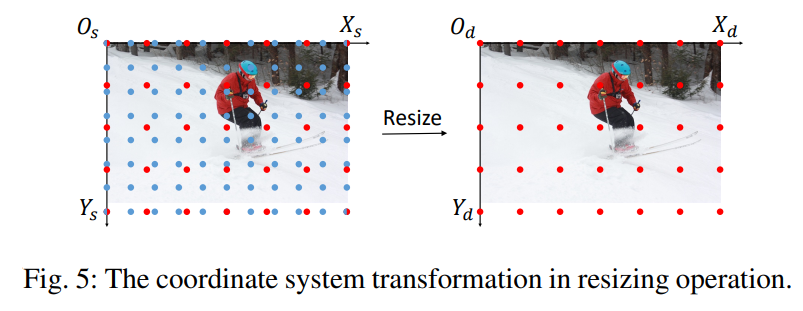
变换矩阵为：

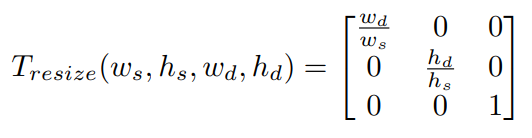
Rotating

旋转操作由于要保护变换后目标仍在图片内，不会由于旋转跑到画幅外，因此通常的操作流程是：先将坐标轴原点移动到ROI中心，然后以新坐标轴原点进行旋转，旋转结束后，用第一步移动坐标轴变换的逆变换，将坐标轴还原。

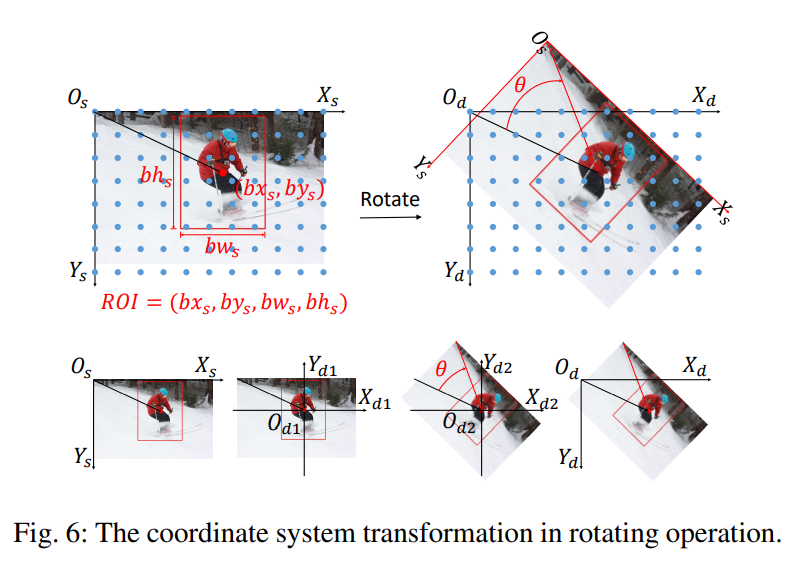
由于实际经历了三个变换，变换矩阵也由三部分构成：

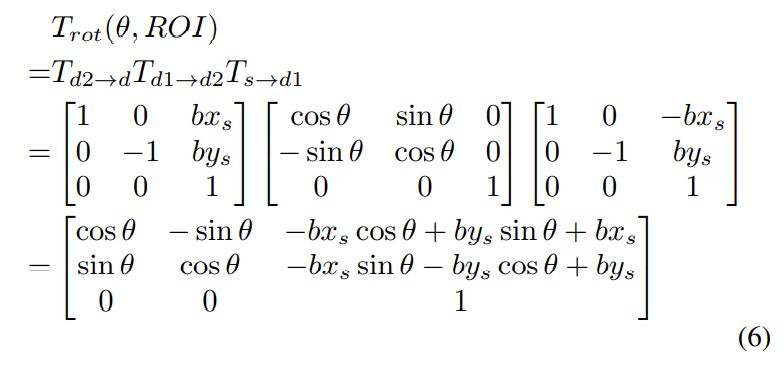
Flipping

水平翻转只需要以图片宽度的一半为轴进行镜像即可：

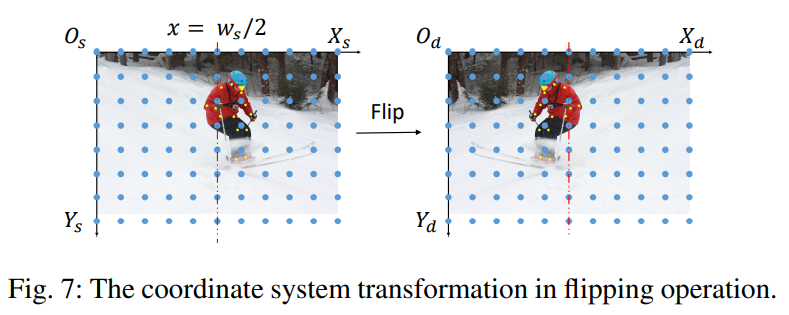
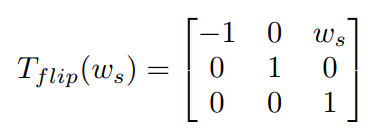
误差验证

用新定义的坐标系和变换矩阵，我们可以从数学上证明，原本水平翻转出现的对齐问题被消除了。

在输出坐标到原始图像上的变换是一致的：

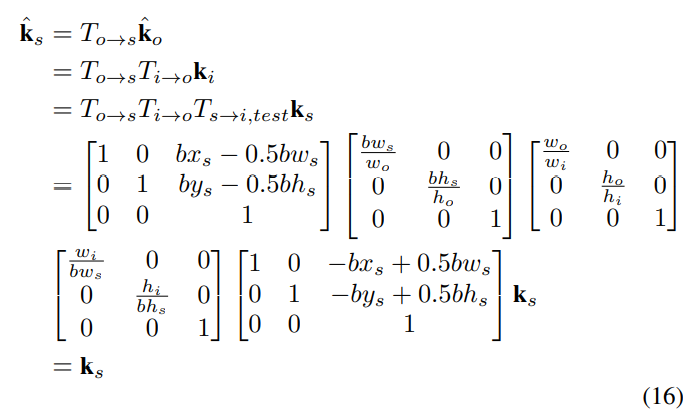
在输出结果上的翻转变换结果也与标注信息一致：

那么，假如用原来的离散坐标系代入变换会怎么样呢？

输出到原始图片的变换结果仍然是一致的，这说明离散坐标系上这部分的变换仍然是无偏的：

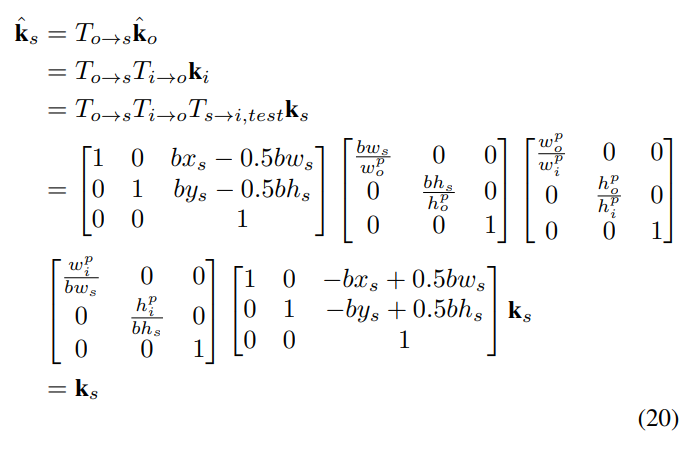
可是涉及翻转的部分：

可以看到，结果有了一个偏移，偏移的距离也已经算出来了，其中等于下采样率。

于是通过翻转集成，最终的结果为：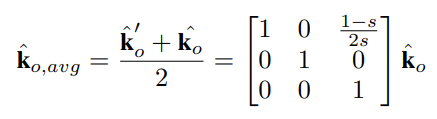

在4倍下采样的模型中，误差可以算出来：

误差修正

前面我们提到，对于这种误差，之前虽然没有人如此明确地计算出来源和数值，但还是有一部分人意识到了它的存在，因而用一些trick来修正这种误差。

过去大家常用的一个trick是，将翻转后的结果移动一个像素，这个变换用矩阵表示为：

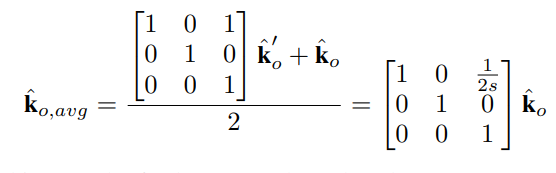
如此一来，通过我们的公式可以验证，最终的集成误差被修正为：

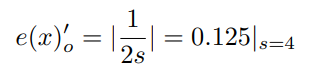
可见，大家之前的做法的确是能从理论上降低误差范围，只是不够彻底罢了。

基于这样一种误差分析和修正的视角，作者进一步发现了另一种误差修正的途径：增大分辨率。

当前我们计算的误差是在输出尺度上的，假如我们映射到原始图片尺度上：

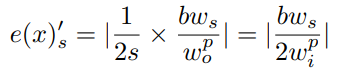
其中是固定的，而输入图片尺寸是我们指定的，这个式子告诉我们，增大输入图片尺寸可以帮助减小误差。

而在没有进行像素偏移修正的情况下误差为：

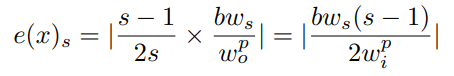
这意味着，增大输入图片分辨率和增大输出图片分辨率（降低下采样率）都可以降低这种误差，这为过去的很多工作能够涨点提供了明确的理论解释。

再回到一开始我设计的例子，对于连续空间中16x16的图片，图片的长宽都为15：

• 原始图片经过Resize到8x8，即图片长宽变为7，因此标注点(8, 8)变为8 * 7 /15 = 3.73

• 进行一次水平翻转操作，即以x=3.5为轴进行镜像，坐标计算得到(3.27, 3.73)

• 采样点经过4倍下采样，2x2特征图对应的图片长宽为1，因此坐标缩小7倍，坐标变为(0.47, 0.53)，由于模型输出的结果只能是整数，那么在这个只有0和1两个坐标值的坐标系里，因为0.47 < 0.5，x坐标0对应的特征图像素上响应值会更大，y坐标对应1，因而模型输出解码为(0, 1)

• 再次水平翻转，以x=0.5为轴进行对称，模型翻转预测的结果为(1, 1)，与我们的设想吻合，翻转引入的误差被消除了

关键点编解码误差

本文立足于无偏数据处理，因此要把整个姿态估计中涉及的所有误差都梳理一遍，而关键点编解码过程中也有一类常见的误差，过去我们经常称为量化误差(quantization error)。

简单来说，由于Heatmap-based方法分为编码和解码两个步骤，编码是把坐标值渲染成对应位置的高斯概率分布，解码是把模型输出的高斯概率分布图用Argmax得到最大相应点坐标。

而Argmax操作最致命的问题在于，它的结果只能是整数。

这就导致了经过下采样的特征图永远不可能得到输入图片尺度的坐标精度，毕竟，输入图片上的整数坐标对应到输出尺度上就带小数了，而Argmax会抹去这个小数，因而产生了误差。

更具体地讲，这种低分辨率导致的问题在于，输出的特征图上最大响应值点坐标并不能正好对应高斯分布的极值点，它们之间存在一个小于1个像素的偏差，由于分辨率低无法表现出来。

对于这一类误差，同样有两种误差修正方案：

• 分类形式

• 分类+回归形式

分类形式

分类形式的误差修正是当前SOTA方案中最广泛运用的，来自于非常有名的Darkpose工作。

简单来说，由于Heatmap-based方法的Target和Output都是基于高斯分布假设的，而高斯分布的形状和参数我们都预先设定好了，也就是说，我们完全可以根据理论上的高斯分布形状，对输出的低分辨率的结果进行信息补全。

这应该不难理解，在所有参数和分布已知的情况下，高斯分布的形状对我们来说就像有一张无限高分辨率的模板图，而模型输出的是这个模板的低分辨率图，我们完全可以通过比对手里的高清图，来找到理论上的高斯分布极值点坐标，从而将低分辨率Argmax抹去的小数恢复出来。

而这种信息补全的手段，正是泰勒展开。

对于泰勒展开的思想，简单来说就是，函数图像上每一个点，由于点是连续的，因而都蕴含着关于周围点的信息，通过该点的一阶导数，我们可以知道下一个点会比这个点高还是低，通过二阶导数，我们可以知道一阶导数的变化趋势，也就是这种升高和降低的力度变化，理论上来说阶数越高我们能还原出来的信息就越多，从而越逼近真实函数值。

由于高斯分布是我们已知的信息，所以我们很容易就能求出输出图像最大值点上的一阶导数和二阶导数，从而对结果进行信息补充，在一定范围内修正量化误差。

写成表达式为：

什么，你问为啥只求到二阶导数？因为高斯分布函数最高只有二阶导（摊手）。

关于Darkpose更详细的解读可以看一下这篇文章：

https://zhuanlan.zhihu.com/p/509670435

在本文中作者还对这种误差修正方法的理论误差进行了计算，在这里我就不写了，感兴趣的小伙伴可以阅读原文。总体而言，这种修正是有局限的，通过二阶泰勒展开能找回的信息毕竟还是存在理论误差的，因此只是一定程度上的修正。

分类+回归形式

分类+回归的形式在我过去的文章中都有介绍过了，有的称之为offset-based方法，也可以理解成“检测+回归”，或者“粗定位+细补充”。

简单来说就是在Heatmap定位的同时，还计算一个回归头部，预测Heatmap极值点跟真实GT的偏移，因而最终模型的预测是定位+回归合并的结果。

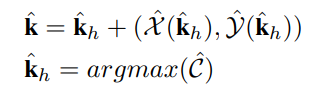
需要指出的是，这种形式并非本文原创，但却使用得非常合理。这种形式从理论上消除了算法设计上的量化误差，让误差完全来自于模型的预测精度本身。

实验结果

最后照例卖一下结果：

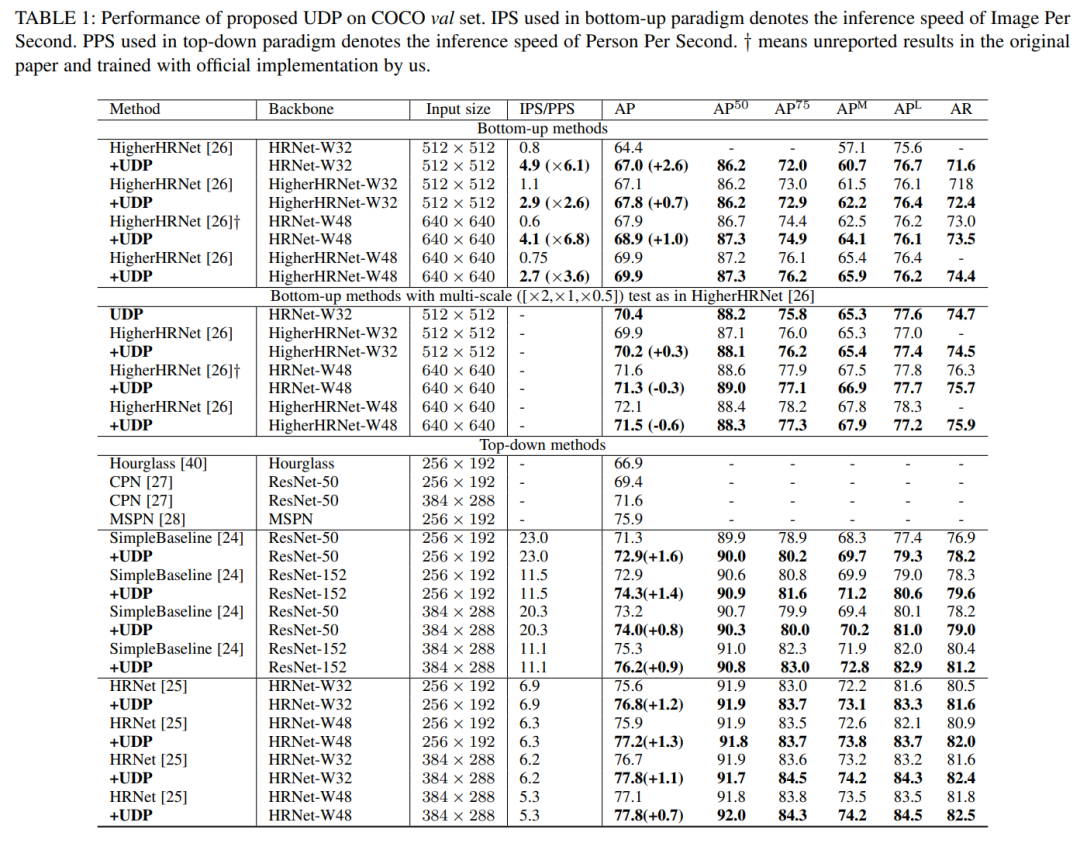
在理解了本文核心思想后，可以明白这种精度提升是显而易见的。

以上就是关于UDP的笔记内容了，我认为本文的工作是非常solid的，对于后续的模型设计起到了非常深远的影响，而且揭示了本质，无愧为一篇经典之作。关于坐标系设计引入的误差这一点，理解起来也花费了我一些时间，作者重写的版本相较于第一版也清晰详细了很多，我设计的那个小例子希望可以帮到大家。假如发现我有说错的地方，也欢迎批评指正和交流。