绑定手机号
确认绑定
0
0
双重视角下的 Linear Attention：为什么 Chunkwise并行是必经之路
分类：
AI技术解析
2026-01-21 06:00:28 作者：德布劳钦
地址：https://zhuanlan.zhihu.com/p/1993761603728982514
经授权发布，如需转载请联系原作者
在长文本生成场景中，标准 Transformer 的推理成本随序列长度平方级增长，这促使研究者探索各种替代方案。Linear Attention 是其中颇具代表性的一类方法，但它常被简化理解为「用特征映射替代 softmax 的 Attention」。
这种理解虽然直观，却容易让人忽略 Linear Attention 在计算结构上的本质变化。如果不深入理解这一点，就很难回答三个关键问题：
为什么它在推理阶段如此高效？
为什么在训练阶段反而容易成为瓶颈？
以及，为什么 chunkwise 并行几乎是必经之路？
本文从Attention 视角与 RNN 视角 两个互补角度出发，逐步推导 Linear Attention 的计算形式，并说明如何融合这两种视角，设计出兼顾因果性与并行效率的 chunkwise 方案。
01 从 Attention 视角诠释 Linear Attention
为简化讨论，仅考虑单头注意力。设输入为：
经过线性投影后得到：
忽略 scale 因子，标准 Attention 可写为：
而在不引入核函数的最简形式下，Linear Attention 则变为：
在这种写法中，Linear Attention 仍然可以被理解为：先计算 attention score (QKT)，再用该 score 对 V 做加权求和。这使得它在建模形式上与标准 Attention 非常接近，也自然继承了一个重要优点：causal mask 的实现极其直接。只需在 attention score 上施加上三角 mask，即可保证因果性。
正因如此，Attention 视角在训练/prefill 阶段表现出色：
所有的 attention score 都可以在一个矩阵乘里完成计算
仅用一个 mask 就能保证因果性
计算高度并行，容易吃满 Tensor Core
然而，在 decode 阶段，这个视角的问题同样明显，每生成一个新 token，都需要对历史所有的 K、V 进行查询。这直接导致：
KV cache 线性增长，显存占用与序列长度成正比
访存带宽成为瓶颈，即便批量很小也难以提速
即便引入 KV cache 量化、前缀匹配、稀疏注意力等工程手段，也只能缓解症状，无法改变“历史 KV 必须被反复访问”这一结构性事实。
02 从 RNN 视角诠释 Linear Attention
Linear Attention 的关键特性在于，attention score 在 sequence 维度上没有非线性操作（如 softmax）。这意味着我们可以利用矩阵乘法的结合律，对计算顺序进行重排。
原始公式可以改写为：
对于第 i 个 token 来说，有：
定义隐藏状态：
则可得到递推关系：
这就是一个典型的 RNN 形式：每个时间步维护一个定长隐藏状态 ，通过递推更新。
从 RNN 视角来看，推理阶段的访存与计算都比较友好：
K^T · V 的 shape 永远是[head_dim, head_dim]，KV cache 不再随 seq_len 增长。
计算复杂度也从 O(seq_len * seq_len * head_dim) 变成了 O(seq_len * head_dim * head_dim)。从推理系统的角度看，是有明显的优势的。
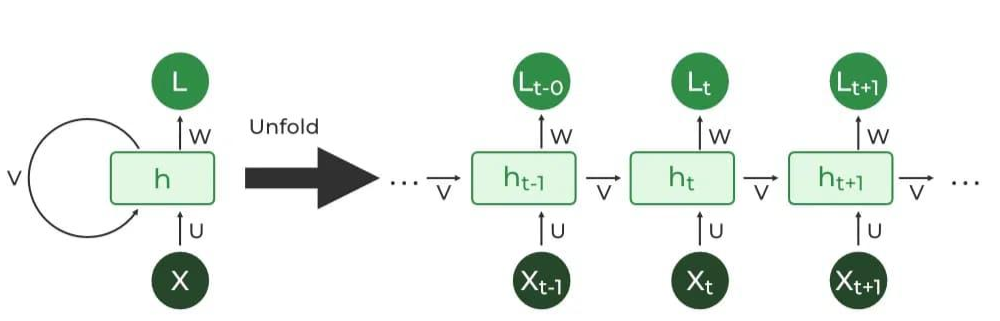
那么，为什么 RNN 视角在训练阶段反而成为问题？根源在于因果约束与递推依赖的冲突。
在训练 / prefill 阶段：
每个 Hi 都依赖于 Hi-1，形成严格的序列依赖
无法像标准 Attention 那样，对整个序列一次性并行计算
这意味着 Attention 阶段的并行度受限，也无法利用 Tensor Core 的计算能力进行加速。其根本原因并不在算子本身，而在于 RNN 计算图的并行性上限。
03 Chunkwise Parallel：融合双重视角的高效方案
既然 Linear Attention 可以从两个视角诠释，且各有利弊，一个自然的想法是：能否融合两种视角，在保持因果性的前提下提升并行度？
答案是肯定的。关键洞察在于：Linear Attention 在 sequence 维度上的线性性，允许我们对 attention score 进行分块拆解。这正是 chunkwise linear attention 的核心思想。
1. 基本思路
将长度为 seq_len 的序列划分为多个 chunk，每个 chunk 长度为 chunk_len：
chunk 间：使用 RNN 视角，递推隐藏状态
chunk 内：使用 Attention 视角，充分并行计算
2. 2-pass 计算流程
Pass 1：Inter-chunk（RNN 视角），递归计算每个 chunk 之前的隐藏状态 H，进而计算 chunk 之间的注意力结果
对第 i 个 chunk，计算其内部的累积状态：
在 chunk 维度上进行 cumsum，得到每个 chunk 的前序累积状态
计算 inter-chunk 输出，得到：
Pass 2：Intra-chunk（Attention 视角），并行计算每个 chunk 内部的注意力结果
在 chunk 内施加 causal mask（上三角 mask）
在 chunk 内按照 attention score 的方式计算 attention：
最终结果：out = inter + intra
值得一提的是，为什么 Linear Attention 可以通过 chunkwise 的划分，将 attn_out 划分为 inter_attn_out + intra_attn_out？谜底就在谜面上，因为这是 Linear Attention，在 attention score 的 seq_len 的 dim 上不存在非线性。所以从矩阵乘法的角度上，才可以进行这样的划分。后面会有严格的数学推导。
代码可以简单的表示为：
def torch_chunk_linear_attn(q, k, v, chunk_size=64):
# 重塑为 chunk 形式：(batch, head, num_chunks, chunk_size, head_dim)
q = rearrange(q, 『b h (n C) d -> b h n C d』, C=chunk_size) * (q.shape[-1] ** -0.5)
k = rearrange(k, 『b h (n C) d -> b h n C d』, C=chunk_size)
v = rearrange(v, 『b h (n C) d -> b h n C d』, C=chunk_size)
# Pass 1: Inter-chunk (RNN 视角)
# 计算每个 chunk 的 K^T V
kv = k.transpose(-1, -2) @ v # (b, h, n, head_dim, head_dim)
# 在 chunk 维度上累积求和
kv = kv.cumsum(2) # cumsum 沿 num_chunks 维度
# Shift 操作：确保每个 chunk 只能看到之前的累积状态
# 当前 chunk 不应看到自身的 KV
kv = torch.cat([
torch.zeros_like(kv[:, :, :1]), # 第一个 chunk 前无历史
kv[:, :, :-1] # 其余 chunk 使用前一个的累积
], dim=2)
# 计算 inter-chunk 输出
inter = q @ kv # (b, h, n, C, d) @ (b, h, n, d, d) -> (b, h, n, C, d)
# Pass 2: Intra-chunk (Attention 视角)
# 计算 chunk 内的 causal attention
attn_mask = torch.triu(torch.ones(chunk_size, chunk_size, dtype=bool, device=q.device), diagonal=1)
intra = ((q @ k.transpose(-1, -2)).masked_fill_(attn_mask, 0)) @ v
# 合并两部分输出
o = inter + intra
return rearrange(o, 『b h n C d -> b h (n C) d』)04 数学推导：为什么可以out = inter + intra？
考虑将序列分为两个 chunk：[0,C) 和 [C,2c)。对于第二个 chunk 中的第 i 个 token（全局位置为 C+i），其输出应为：
可以拆解为：
定义：
则最终输出为：
最后，还是和之前说的一样，这种拆解之所以成立，正是因为 Linear Attention 不含 softmax——在矩阵乘法层面，线性性保证了求和顺序可交换。
参考
Gated Linear Attention Transformers with Hardware-Efficient Training
flash-linear-attention 中的 Chunkwise 并行算法的理解
